Tree data structure

Tree Data Structure

Tree data structure is defined as a collection of objects or entities known as nodes that are linked together to represent or simulate hierarchy.
A tree data structure is a non-linear data structure because it does not store in a sequential manner. It is a hierarchical structure as elements in a Tree are arranged in multiple levels.
In the Tree data structure, the topmost node is known as a root node. Each node contains some data, and data can be of any type.
Each node contains some data and the link or reference of other nodes that can be called children.

Some basic terms used in Tree data structure.

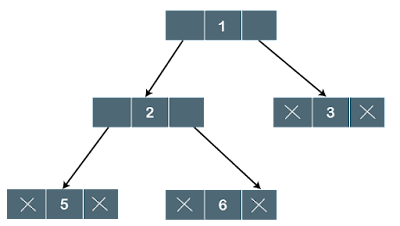
Let's consider the tree structure, which is shown below:

In the above structure, each node is labeled with some number. Each arrow shown in the above figure is known as a link between the two nodes.

Root: The root node is the topmost node in the tree hierarchy.
Child node: The node below a given node connected by its edge downward is called its child node
Parent: If the node contains any sub-node, then that node is said to be the parent of that sub-node.
Sibling: The nodes that have the same parent are known as siblings.
Leaf Node:- The node of the tree, which doesn't have any child node, is called a leaf node.
Internal nodes: A node has at least one child node known as an internal.

Types of Tree data structure

The following are the types of a tree data structure:

General tree

Binary Tree

Binary Search Tree

General tree: The general tree is one of the types of tree data structure. In the general tree, a node can have either 0 or maximum n number of nodes. There is no restriction imposed on the degree of the node (the number of nodes that a node can contain). The topmost node in a general tree is known as a root node. The children of the parent node are known as subtrees.

There can be n number of subtrees in a general tree. In the general tree, the subtrees are unordered as the nodes in the subtree cannot be ordered.

Every non-empty tree has a downward edge, and these edges are connected to the nodes known as child nodes. The root node is labeled with level 0. The nodes that have the same parent are known as siblings.

Binary tree:

The Binary tree means that the node can have maximum two children. Here, binary name itself suggests that 'two'; therefore, each node can have either 0, 1 or 2 children.

The above tree is a binary tree because each node contains the utmost two children. The logical representation of the above tree is given below:

In the above tree, node 1 contains two pointers, i.e., left and a right pointer pointing to the left and right node respectively. The node 2 contains both the nodes (left and right node); therefore, it has two pointers (left and right). The nodes 3, 5 and 6 are the leaf nodes, so all these nodes contain NULL pointer on both left and right parts.

Binary Tree Traversal

Traversal is a process to visit all the nodes of a tress. There are 3 methods to traverse a binary tree.

1. In Order Traversal

2. Pre Order Traversal

3. Post Order Traversal

1. In Order Traversal

Traverse the left subtree, i.e., call Inorder(left->subtree)
Visit the root.
Traverse the right subtree, i.e., call Inorder(right->subtree)

2. Pre Order Traversal

Algorithm Preorder(tree)

Visit the root.
Traverse the left subtree, i.e., call Preorder(left->subtree)
Traverse the right subtree, i.e., call Preorder(right->subtree)

3. Post Order Traversal

Algorithm Postorder(tree)

Traverse the left subtree, i.e., call Postorder(left->subtree)
Traverse the right subtree, i.e., call Postorder(right->subtree)
Visit the root

Binary Search tree

A binary search tree follows some order to arrange the elements. In a Binary search tree, the value of left node must be smaller than the parent node, and the value of right node must be greater than the parent node. This rule is applied recursively to the left and right subtrees of the root.

Let's understand the concept of Binary search tree with an example.

In the above figure, we can observe that the root node is 40, and all the nodes of the left subtree are smaller than the root node, and all the nodes of the right subtree are greater than the root node.
Similarly, we can see the left child of root node is greater than its left child and smaller than its right child. So, it also satisfies the property of binary search tree. Therefore, we can say that the tree in the above image is a binary search tree.
Suppose if we change the value of node 35 to 55 in the above tree, check whether the tree will be binary search tree or not.

In the above tree, the value of root node is 40, which is greater than its left child 30 but smaller than right child of 30, i.e., 55. So, the above tree does not satisfy the property of Binary search tree. Therefore, the above tree is not a binary search tree.

Example of creating a binary search tree

Now, let's see the creation of binary search tree using an example.

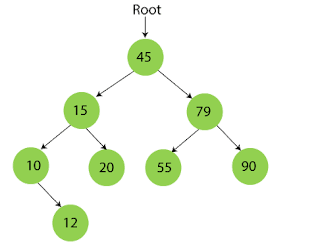
Suppose the data elements are - 45, 15, 79, 90, 10, 55, 12, 20, 50

First, we have to insert 45 into the tree as the root of the tree.
Then, read the next element; if it is smaller than the root node, insert it as the root of the left subtree, and move to the next element.
Otherwise, if the element is larger than the root node, then insert it as the root of the right subtree.

Now, let's see the process of creating the Binary search tree using the given data element. The process of creating the BST is shown below -

Step 1 - Insert 45.

Step 2 - Insert 15.

As 15 is smaller than 45, so insert it as the root node of the left subtree.

Step 3 - Insert 79.

As 79 is greater than 45, so insert it as the root node of the right subtree.

Step 4 - Insert 90.

90 is greater than 45 and 79, so it will be inserted as the right subtree of 79.

Step 5 - Insert 10.

10 is smaller than 45 and 15, so it will be inserted as a left subtree of 15.

Step 6 - Insert 55.

55 is larger than 45 and smaller than 79, so it will be inserted as the left subtree of 79.

Step 7 - Insert 12.

12 is smaller than 45 and 15 but greater than 10, so it will be inserted as the right subtree of 10.

Step 8 - Insert 20.

20 is smaller than 45 but greater than 15, so it will be inserted as the right subtree of 15.

Step 9 - Insert 50.

50 is greater than 45 but smaller than 79 and 55. So, it will be inserted as a left subtree of 55

Now, the creation of binary search tree is completed. After that, let's move towards the operations that can be performed on Binary search tree.

We can perform insert, delete and search operations on the binary search tree.

Let's understand how a search is performed on a binary search tree.

Searching in Binary search tree

Searching means to find or locate a specific element or node in a data structure. In Binary search tree, searching a node is easy because elements in BST are stored in a specific order. The steps of searching a node in Binary Search tree are listed as follows -

First, compare the element to be searched with the root element of the tree.
If root is matched with the target element, then return the node's location.
If it is not matched, then check whether the item is less than the root element, if it is smaller than the root element, then move to the left subtree.
If it is larger than the root element, then move to the right subtree.
Repeat the above procedure recursively until the match is found.
If the element is not found or not present in the tree, then return NULL.

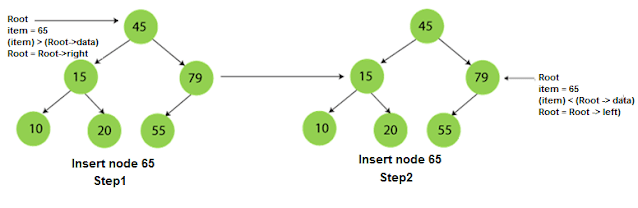
Now, let's understand the searching in binary tree using an example. We are taking the binary search tree formed above. Suppose we have to find node 20 from the below tree.

Step1:

Step2:

Step3:

Now, let's see the algorithm to search an element in the Binary search tree.

Algorithm to search an element in Binary search tree

Search (root, item)
Step 1 - if (item = root → data) or (root = NULL)
return root
else if (item < root → data)
return Search(root → left, item)
else
return Search(root → right, item)
END if
Step 2 - END

Deletion in Binary Search tree

In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -

The node to be deleted is the leaf node, or,
The node to be deleted has only one child, and,
The node to be deleted has two children

We will understand the situations listed above in detail.

When the node to be deleted is the leaf node

It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.

We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.

When the node to be deleted has only one child

In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.

We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.

So, the replaced node 79 will now be a leaf node that can be easily deleted.

When the node to be deleted has two children

This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -

First, find the inorder successor of the node to be deleted.
After that, replace that node with the in order successor until the target node is placed at the leaf of tree.
And at last, replace the node with NULL and free up the allocated space.

The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.

We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.

Follow the below steps to solve the problem:

If the root is NULL, then return root (Base case)
If the key is less than the root’s value, then set root->left = deleteNode(root->left, key)
If the key is greater than the root’s value, then set root->right = deleteNode(root->right, key)
Else check
- If the root is a leaf node then return null
- else if it has only the left child, then return the left child
- else if it has only the right child, then return the right child
- else set the value of root as of its inorder successor and recur to delete the node with the value of the inorder successor
Return

Insertion in Binary Search tree

A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.

About Me

Dr. Ajay Dutta