Search

 Searching is the process of finding some particular element in the list. If the element is present in the list, then the process is called successful, and the process returns the location of that element. Otherwise, the search is called unsuccessful.

Linear Search and Binary Search are the two popular searching techniques. Here we will discuss the Binary Search Algorithm.

Binary search

Binary search is the search technique that works efficiently on sorted lists. Hence, to search an element into some list using the binary search technique, we must ensure that the list is sorted.

Binary search follows the divide and conquer approach in which the list is divided into two halves, and the item is compared with the middle element of the list. If the match is found then, the location of the middle element is returned. Otherwise, we search into either of the halves depending upon the result produced through the match.

1. Binary_Search(a, lower_bound, upper_bound, val) // 'a' is the given array, 'lower_bound' is the index of the first array element, 'upper_bound' is the index of the last array element, 'val' is the value to search  
2. Step 1: set beg = lower_bound, end = upper_bound, pos = - 1  
3. Step 2: repeat steps 3 and 4 while beg <=end  
4. Step 3: set mid = (beg + end)/2  
5. Step 4: if a[mid] = val  
6. set pos = mid  
7. print pos  
8. go to step 6  
9. else if a[mid] > val  
10. set end = mid - 1  
11. else  
12. set beg = mid + 1  
13. [end of if]  
14. [end of loop]  
15. Step 5: if pos = -1  
16. print "value is not present in the array"  
17. [end of if]  
18. Step 6: exit  

Working of Binary search

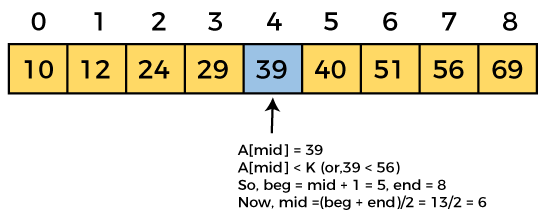
Let the elements of array are -

Let the element to search is, K = 56

We have to use the below formula to calculate the mid of the array

mid = (beg + end)/2  

So, in the given array -

beg = 0

end = 8

mid = (0 + 8)/2 = 4. So, 4 is the mid of the array.

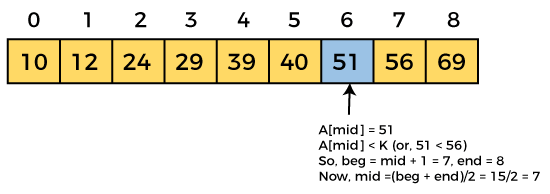
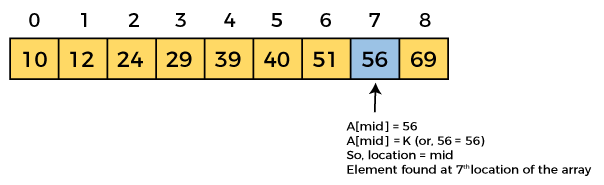
Now, the element to search is found. So algorithm will return the index of the element matched.

Linear Search Algorithm

Linear search is also called as sequential search algorithm. It is the simplest searching algorithm. In Linear search, we simply traverse the list completely and match each element of the list with the item whose location is to be found. If the match is found, then the location of the item is returned; otherwise, the algorithm returns NULL.

It is widely used to search an element from the unordered list, i.e., the list in which items are not sorted. The worst-case time complexity of linear search is O(n).

The steps used in the implementation of Linear Search are listed as follows -

• First, we have to traverse the array elements using a for loop.
• In each iteration of for loop, compare the search element with the current array element, and -
  • If the element matches, then return the index of the corresponding array element.
  • If the element does not match, then move to the next element.
• If there is no match or the search element is not present in the given array, return -1.

Working of Linear search

Now, let's see the working of the linear search Algorithm.

To understand the working of linear search algorithm, let's take an unsorted array. It will be easy to understand the working of linear search with an example.

Let the elements of array are -

Let the element to be searched is K = 41

Now, start from the first element and compare K with each element of the array.

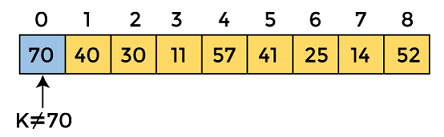
The value of K, i.e., 41, is not matched with the first element of the array. So, move to the next element. And follow the same process until the respective element is found.

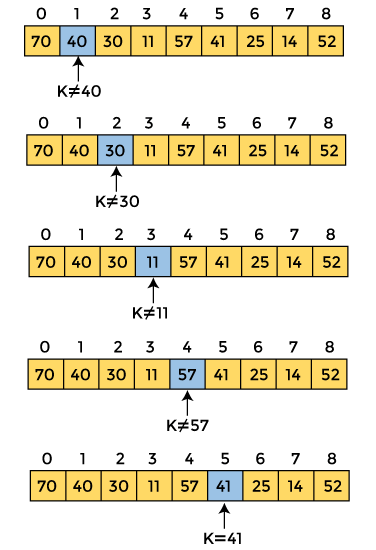
Now, the element to be searched is found. So algorithm will return the index of the element matched.